直方图(Histogram)
直方图(Histogram) 是 QC 七大手法中最基础也最常用的统计工具之一,用于展示数据的分布形态(Distribution),反映出制程的稳定性、离散程度、集中趋势以及是否存在偏态、双峰、混合模式等问题。
直方图的核心价值在于:让复杂的统计数据变成一眼看懂的图形,让人直观地看到“数据真正长什么样”。
这对质量工程师、生产主管、六西格玛黑带与 精益改善 团队来说,是判断质量问题的第一步。
在 六西格玛 DMAIC 的定义、测量、分析阶段中,直方图都是必不可少的基础工具。
一、什么是直方图?(Histogram 的概念)
直方图是一种将连续型数据分组(分箱)后,以柱状条显示每组数据出现频率(或相对频率)的统计图形。
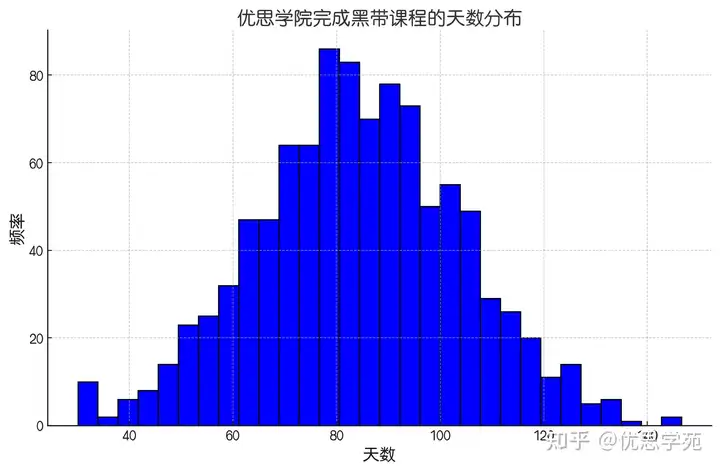
它可以回答几个关键问题:
- 数据是否呈正态分布?
- 是否有偏态(左偏 / 右偏)?
- 是否有多个峰值(双峰、多峰)?
- 是否存在异常群体?(例如操作员 A 与操作员 B 所产生的数据混合)
- 数据的离散程度如何?(标准差大 / 小)
- 制程是否稳定可控?
很多时候,直方图能指出问题,而不是结果。例如:
当你看到“二峰分布”,你就知道制程很可能来自两个不同的设备、模具、批次或操作员。
二、直方图由哪些部分组成?
一个标准的直方图包括以下结构:
- 横轴(X 轴):数据的数值区间(如尺寸、重量、扭力、电压)
- 纵轴(Y 轴):数据出现的频率或相对频率
- 分组 / 分箱(Bins):将数据按区间划分的组数
- 柱状条(Bars):显示每一组数据出现的次数
- 总体分布形态:正态?偏态?双峰?
此外,在质量管理中,直方图经常会叠加:
- 规格上下限(USL、LSL)
- 目标值(Target)
- 平均值(Mean)
这样可以让质量工程师快速判断制程是否满足规格,是否可能会出现不合格品。
三、直方图的适用情境
直方图适用于所有连续型数据分析,包括:
- 尺寸(长度、厚度、直径、间隙)
- 重量
- 压力 / 电流 / 电压
- 扭力
- 温度
- 循环时间
- 测试结果数值
在以下场景中尤其重要:
- 制程能力分析(Cp、Cpk)前
- SPC 控制前
- 六西格玛数据分析前
- 判断是否需要分层取样(Stratification)
任何质量工程师(QE、SQE、PQE、NPI QE、TE)在谈 Cpk 之前,都应该先画直方图确认数据是否呈现单一稳定分布。
四、如何制作直方图?(步骤说明)
步骤 1:收集连续型数据
- 至少需要 30 笔以上的数据(越多越好)
- 数据需来自相同条件:同机台、同模具、同操作员、同批次等
- 若条件混合,必须先进行“分层法”
步骤 2:确定分组方式(分箱 Bins)
常见经验法则:
- √n 法(例如 n=100,则用 10 个分组)
- Sturges公式 或 Scott规则(统计软件会自动决定)
步骤 3:绘制直方图
常用工具包括:
- Excel
- Minitab(六西格玛常用软件)
- Python(matplotlib / seaborn)
- JMP、SPSS、R
步骤 4:加上规格限与平均值(若用于质量管理)
- 加入 LSL / USL
- 加入 Target(目标值)
- 加入平均值(Mean)
步骤 5:判断分布形态
查看图形后再进行分析。
五、常见的直方图分布形态与意义
直方图最强大的地方在于,它能揭露“问题的形状”。
1. 正态分布(单峰、居中、对称)
这是理想的制程状态:
- 数据在平均值左右呈对称分布
- 无偏态
- 无多峰
- 制程通常比较稳定
可进入 Cp、Cpk 计算与 SPC 管制。
2. 偏态分布(左偏 / 右偏)
可能原因:
- 模具磨耗
- 夹具定位偏差
- 设备老化
- 参数设定偏离目标
偏态的制程能力往往不佳,需要改善。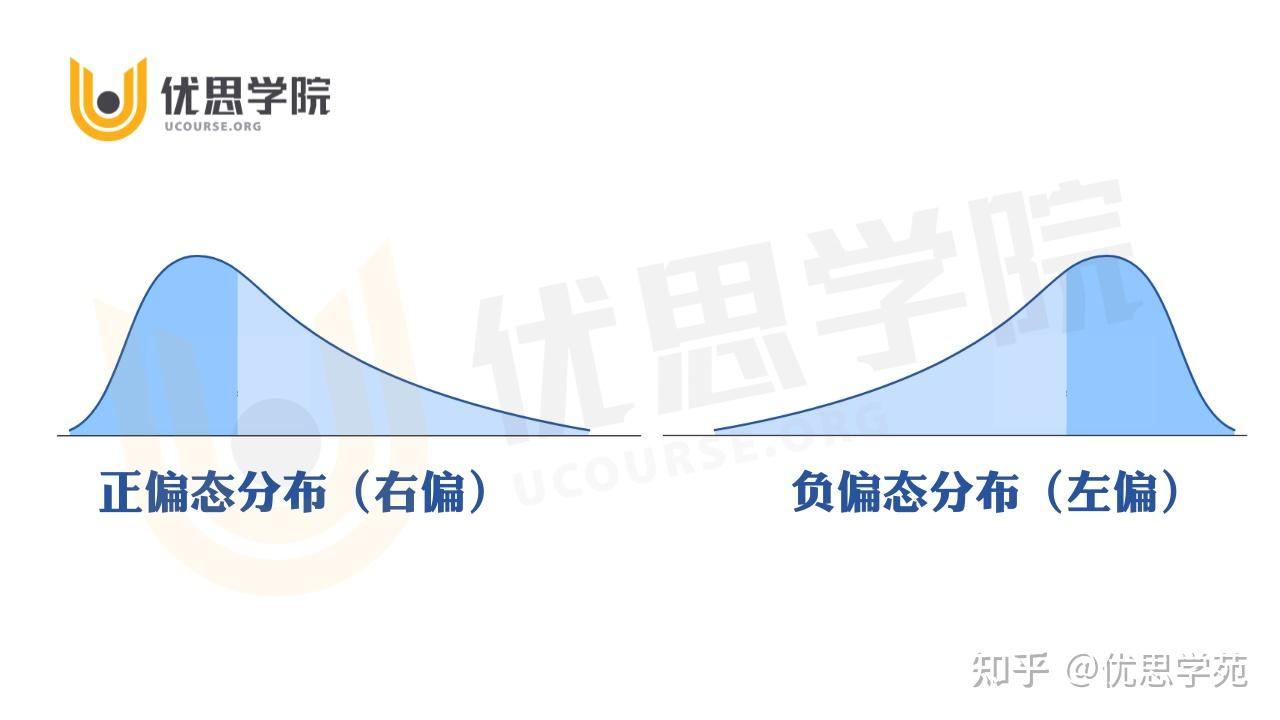
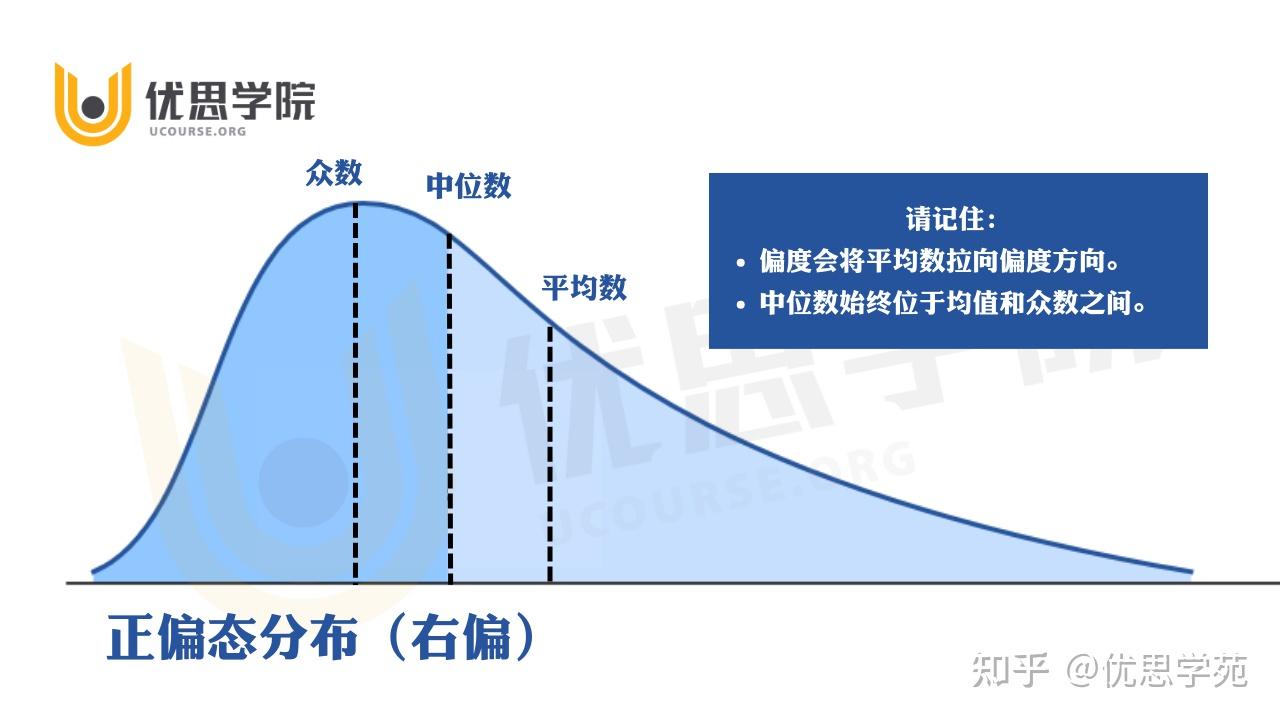
3. 双峰 / 多峰分布(Bimodal / Multimodal)
最典型的“制程混合”信号。
可能原因:
- 两个模具
- 两位不同操作员
- 两台不同机台
- 两个批次的材料混合
- 量测系统不一致(不同量具 / 检验员)
在六西格玛中,看到双峰分布时,第一动作应该是:
立即分层(Stratify)。
4. 截断分布(Truncated)
若大量数据贴近规格限,观察到“截断”形状:
- 人为筛选(挑选)
- 测量系统无法量到真实值(下限)
- 设备设定已逼近机械极限
5. 平顶分布(Uniform / Plateau)
常表示:
- 多批次混合
- 数据区间宽广但没有明显趋势
- 量测方法不稳定
6. 离散点或间断分布
若数据分布呈“阶梯状”或“明显只有几个值”,常表示:
- 量具分辨率不足(Resolution 不够)
- 数据取整导致失真
- 量具或方法不合适
若数据呈阶梯状,通常 MSA(量测系统分析) 需要优先进行。
六、直方图在质量管理中的重要性
直方图不仅仅是一张图,它是许多质量决策的基础。
1. 用于判断制程能力(Cp、Cpk)前的必要步骤
在计算 Cp 或 Cpk 之前,必须确认数据呈现单一、稳定的分布,否则 Cpk 会“造假”。
2. 用于识别制程中的隐藏问题
- 是否存在多个来源(混合)?
- 操作员影响大吗?
- 设备差异大吗?
- 材料批次差异大吗?
直方图能让你在“不知道是什么问题”的时候,从形状中发现线索。
3. 用于改善项目的初步诊断
在六西格玛 DMAIC 中:
- Define:定义问题根源的“形状”
- Measure:确认分布与稳定度
- Analyze:通过分布形态判断可能原因
4. 用于确认分层法(Stratification)是否必要
直方图发现双峰后,应立即根据:
- 设备
- 模具
- 班别
- 供应商
- 操作员
分层重新绘制直方图。
七、直方图的局限性
尽管直方图是强大的工具,但也存在限制:
- 需要足够的数据量
- 结果受分组方式影响
- 无法直接显示趋势(需结合折线图或控制图)
- 无法显示时间排序(需结合运行图 / 控制图)
- 若数据混合,需要先分层,否则误导
因此实际分析时,直方图通常与 SPC 控制图 与箱型图(Boxplot)结合使用。
八、如何让直方图分析更有效?(实战技巧)
以下为一线质量工程师最常用的实战技巧:
技巧 1:永远“先分层再画图”
不要把不同机台、不同供应商、不同批次的数据混在一起,否则直方图没有意义。
技巧 2:配合 Boxplot / Run Chart / Control Chart 一起看
- Boxplot 看分布偏移
- Run Chart 看时间趋势
- SPC 看是否失控
技巧 3:在直方图上加规格限与平均值
帮助判断:数据是否靠近 USL/LSL,是否存在偏移风险。
技巧 4:寻找异常形状(红旗信号)
- 双峰 → 混合
- 长尾 → 偏态
- 尖峰 → 分辨率不足
- 截断 → 接近规格限或人为挑选
九、直方图常见错误
- 样本量太少
- 混合不同来源的资料(未分层)
- 忽略分组方式导致图形变形
- 忽略量测系统不良(未经 MSA)
- 未加入规格限,缺乏质量意义
十、小结:直方图是理解“数据性格”的第一步
直方图(Histogram)是最基础、最直觉、也是最具洞察力的数据分析图表之一。
它展示的不是一串数字,而是“制程的性格”与“问题的形状”。
通过直方图,我们能够:
- 判断制程是否稳定
- 辨识偏态、双峰、截断等风险
- 辅助做出 Cp/Cpk、SPC 等高阶分析
- 洞察可能的机器、材料、人员、方法问题
无论你是质量工程师、供应商质量管理(SQE)、制程工程师(PE)、NPI QE、可靠性工程师(RE),
直方图都是你理解数据、做出判断的第一步。
看图,找形状;找形状,找原因;找原因,才有真正的改善。